В этой заметке я бы хотел рассказать об очередно небольшом прикладном исследовании, которое понадобилось предпринять для того чтобы отыскать наиболее выгодный алгоритм подсчёта того что я дальше буду называть "скользящей статистикой". Я не очень уверен в терминологической корректности, но в зарубежной номенклатуре семейство подобных алгоритмов называется "moving statistics", вы можете видеть описание функций предназначенный для такого счёта в справке по, например, библиотеке GSL.

Поначалу мотивация мне казалась сомнительной -- ну есть же в GSL реализация, а в GSL что попало не попадает. Я сделал прототип, написал юнит-тест, сравниваясь с GSL и оказался неприятно удивлён. Сделалось ясно, что рализация GSL не очень годится для практических рассчётов.

Постановка Задачи

Итак, среди для упорядоченного множества $x_i, i \in \{{0, 1, \ldots N}\}$ требуется посчитать, например, множество средних значений в "окне" шириной $K = H + 1$, которое определим как:

\begin{equation} \hat{\sigma_i} = \frac{1}{J} \sum\limits_{j = i - J - 1}^{i} x_i \end{equation}

То есть, для произвольного $x_i$ выделяется $H$ значений идущих до него, от которых считается среднее. В работе понадобится считать ещё и стандартное отклонение, и, может быть, второй момент, но в этой заметке я пока ограничусь средними.

В GSL "moving statistics" определяется несколько более широко -- там в усреднение включены ещё $H$ значений после $i$, однако это обобщение меня не интересует, поскольку область применения моего алгоритма будет ограничена большим количеством данных поступающих в реальном времени (мы, таким образом, не имеем информации о значениях идущих после $x_i$).

Catastrophic Cancellation

При беглом размышлении над возможными реализациями алгоритмов "скользящей сататистики" обращает на себя внимание прежде всего возможность большой разницы порядков при операциях с числами с плавающей точкой приводящая к проблеме инфляции значений. У меня есть под рукой реализация алгоритма Кляйна (т.н. Generalized Kahan-Babuška-Summation-Algorithm) которая позволяет избежать этой проблемы без попарного суммирования.

Надо заметить, что недостаток инкрементного подсчёта сумм здесь на первый взгляд отсутствует, -- порядок суммы определяется в основном шириной окна ненамного большего (обычно $10^2-10^3$) чем $x_i$. Однако в реализации есть существенная деталь: наивный взгляд подразумевает хранение суммы окна в переменной, которая обновлялась бы каждый раз при рассмотрении $x_i$, при этом, для соблюдения постоянной ширины окна, из суммы нужно вычитать последнее значение $x_{i - J - 1}$. Нетрудно видеть, что в этом случае ошибка $\delta$ суммы $\hat S_i = S_i + \delta$ никуда не исчезает, а будет накапливаться аналогично проблеме при подсчёте прямой суммы.

Без того чтобы помещать $H$ значений в отдельный контейнер обойтись довольно сложно -- их в любом случае понадобится вычитать. Подсчитывать сумму хранимых значений всякий раз не выглядит разумным компромиссом, поскольку налицо вычислительное излишество. Вообще говоря, на ум приходят несколько возможных реализаций, и чтобы выявить наиболее удачную, я произвёл ряд тестов.

Прототип Счётчика

В качестве модельных данных были выбраны значения тангенса с логарифмическим сэмплированием, чтобы с одной стороны гарантировать достаточно широкую вариативность случайной величины по порядку, с другой -- достаточно стабильное среднее.

\begin{equation} x_i = \tan \left( 6 \pi \left(\frac{i+1}{N}\right)^8 \right) \end{equation}

Удобно реализовать алгоритм в виде шаблона параметризуемого типом суммы. Для наглядности я опущу реализацию методов и некоторые вспомогательные поля в классе.

template<typename ScorerT>
class MovingStats : public std::deque<double> {
protected:
    ScorerT _runningSum;
    const size_t _windowSize;
public:
    MovingStats( size_t N );
    virtual double mean() const;
    virtual void account(double sample);
};

Инстанцирование класса требует задания размера окна, затем всякий раз при рассмотрении $x_i$ вызывается account() обновляющий значения суммы записывающий новый образец в конец двусторонней очереди (дека) -- при этом первый элемент очереди удаляется и вычитается из суммы. Метод mean() возвращает текущее значение суммы.

500 чисел

Хотя динамику ошибки хорошо видно на достаточно больших наборах, посмотрим пока $N=500$ с шириной окна $H=10$ -- уже на небольшой выборке хорошо заметна одна интересная особенность, которая, в принципе, и побудила меня сделать эту заметку. На нижнем графике изображены абсолютные ошибки в определении скользящих средних значений по окну $H=10$ (ошибка расчитана против прямой суммы в окне -- в тестах мы можем позволить себе честно посчитать всю сумму каждый раз). Наивной реализации отвечает график $\hat \sigma_i$ -- видно, что он действительно аккумулирует ошибку вызванную большими значениями $x_i$ в районе разрывов функции тангенса. После них она уже не снижается, а небольшие флуктуации нормальны для дискретных отображений. Этого мы, в принципе, и ожидали. Но что неожиданно -- подобное же поведение имеет функция $\hat \sigma_{i, GSL}$! По-видимому внутри функций movstat_gsl_...() используется обычная переменная для суммирования, и они в этом схожи с моей наивной реализацией.

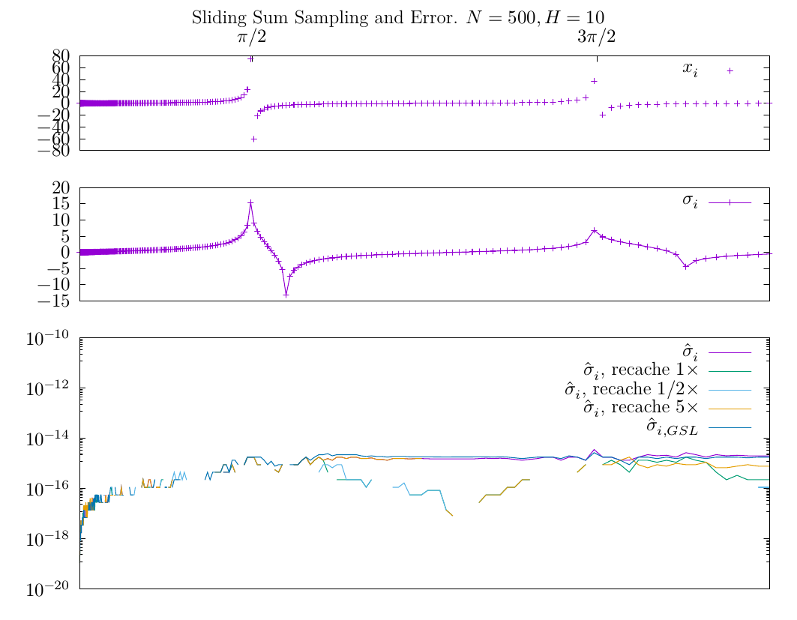
Чтобы убедиться в этом, а так же в качестве пробного средства я снабдил MovingStats::account() проверкой счётчика событий, который вызывает честный пересчёт кэшируемого среднего значения раз в $t\times N$ событий. На иллюстрации изображены графики для $t=1/2$, $t=1$, $t=5$, из которых видно что такой подход в целом позволяет снизить влияние накопления ошибки, хотя и является, вероятно, не самым обоснованным решением снижая детерминизм вычислений.

10 000 чисел

Влияние выбросов и поведение ошибки ещё можно проиллюстрировать на вот этом примере:

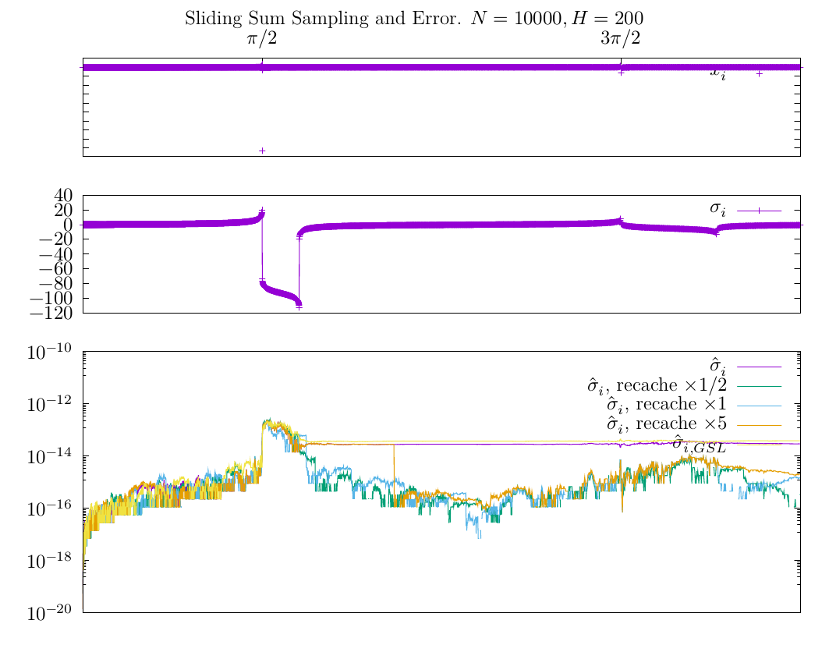
Здесь я специально оставил $x_i \simeq 2 \times 10^4$ возле $\pi/2$ чтобы посмотреть, как такая величина повлияет на ошибку. График ошибки с учётом предыдущего результата не удивляет -- наивная реализация $\hat \sigma_i$ и реализация GSL действительно хранят след такого выброса. Наивная реализация с кэшированием позволяет представить, как выглядел бы счёт избавленный от такого недостатка, однако по графику хорошо видно, что для $i < H$ мы имеем всё то же сомнительное наследие.

Outliers

Предыдущий график подтверждает очевидную мысль, что набиольший вклад в ошибку обусловлен числами значительно превосходящими среднее (в окне) значение. Небольшая модификация счётчика, которая бы могла отслеживать вы-/включение подобных выбросов могла бы существенно изменить дело. С этой целью можно воспользоваться, например, стандартным отклонением и вызывать пересчёт всякий раз когда дэк покидает значение отстоящее от среднего более чем на $3 \sigma$.

Для следующего графика мне понадобилось изменить толщины линий отвечающих разным методам подсчёта средних, поскольку график комбинированного пересчёта суммы ("$\hat \sigma_i$, recache $\times 5$, outl.") сливается с графиком счётчика в котором пересчёт привязан только к выбросам ("$\hat \sigma_i$, recache outl.") -- для выявления возможных различий дисперсия моих данных, очевидно, не слишком велика.

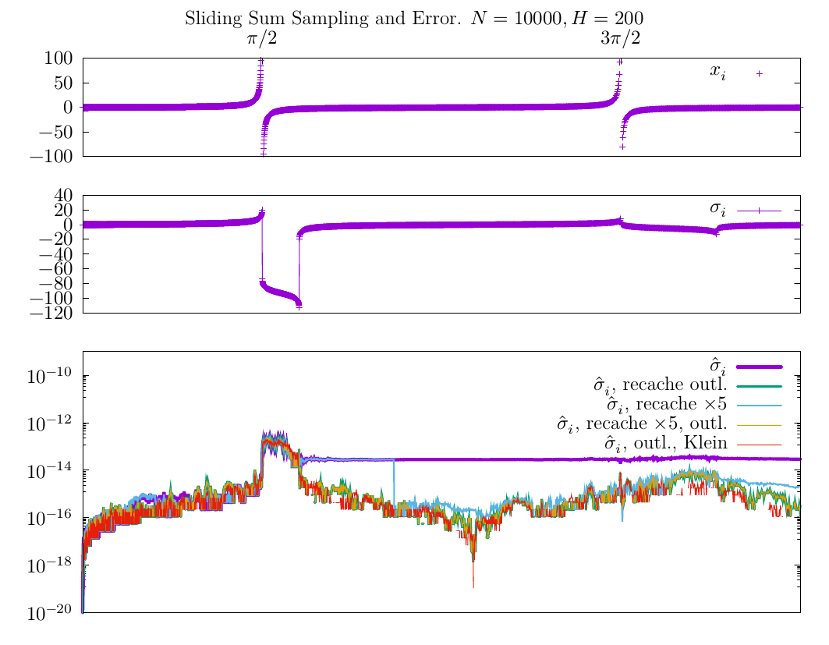
Я также здесь обрезал график $x_i$ исходных данных (верхний) из иллюстративных соображений. Рост ошибки вблизи $\pi/2$ -- по-видимому неизбежное зло, поскольку выброс в четыре-пять порядков существенно превосходящий среднее значение и должен давать в среднем большую ошибку представления вещественного числа. Важный вывод здесь, однако, в том что пересчёт по выбросам (outliers) по-видимому достаточен для численной устойчивости по отношению к, собственно, единичным выбросам. На практике я, наверное, вовсе буду их дискриминировать из исходных данных (график скользящего среднего на второй картинке -- обычно не то что вы ожидаете увидет в онлайн-обработке физических событий).

Последняя кривая на графиках ошибок -- результат применения сумматора по Кляйну вместо обычного типа данных double в шаблонной реализации. По видимому, это возволяет добиться заметно меньшей ошибки при подсчёте сумм даже в окнах на двести элементов.

Заключение

Таким образом алгоритм подсчёта средних значений и дисперсии построенный на двунаправленной очереди в сочетании с сумматором по Кляйну выглядит предлагает достаточно устойчивую реализацию концепции скользящей статистики в сравнении с GSL и наивными реализациями, при этом всё ещё являясь более эффективным с вычислительной точки зрения по сравнению с прямым подсчётом суммы на достаточно равномерных данных (частота вызова вычислительно-дорой процедуры пересчёта скользящей суммы определяется частотой выбросов в статистике исходных данных).